Queue
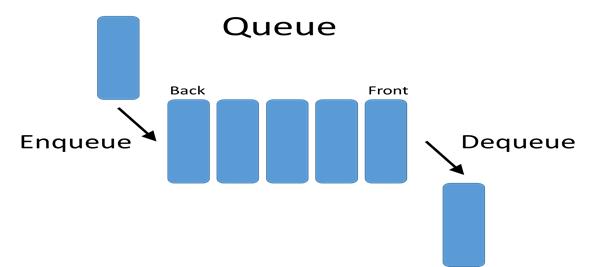
Queue is a non-primitive linear data structure used to represent a linear list. It allows insertion of an element to be made at one end and deletion of an element to be performed at the other end. Queue is a linear list of elements in which deletion of an element can be done only at one end, called the front and insertion can be done at the other end, called the rear.
The first element in a queue will be the first one to be removed from the list. Therefore, queues are also called First In First Out (FIFO) lists. The common examples for queues is the first one to be served.
Many examples of queues can be performed within a computer system there may be queues of tasks waiting for the line printer, for access to disk storage or even, in the time sharing system, for use of the CPU. Within a single program there may be multiple requests to be kept in queue, or one task may create other tasks which must be executed in turn by keeping them in a queue.
Suppose that at a service center,t1 units is needed to provide a service to a single customer and on an average a new customer arrives at service center in t2 units of time. Then there are following possibilities that may arises:
1.If t1 < t2 then the service counter will be free for some time before a new customer arrives at the service counter. Hence there will be np customer standing at a particular time in the queue, or the queue will be empty.
2.If t1>t2 the service counter will be busy for some time even after the arrival of a new customer .therefore the new customers have to wait for some time. This procedure when continues for some time gives rise to a queue.
3.If t1=t1 then as one customer leaves the counter other will arrives at the same instant, hence queue will be single element long.
we insert an element in the queue ,the value of rear incremented by one.
front=Front+1
Rear=Rear+1Whenever an element is removed or deleted from the queue value of front incremented by one i.e.
front=Front+1
Note that during the insertion of the first element in the queue we always increment the Front by one i.e.
QUEUES AS AN ABSTRACT DATA TYPE
A queue of elements of type A is a finite sequence of elements of A together with the following operations:
- Initialize a queue to be empty.
- Determine if a queue is empty or not.
- Determine if a queue is full or not.
- Insert a new element after the last element in a queue, If it is not full.
- Retrieve the first element of a queue, if it is not empty.
- Delete the first element in a queue, if it is not empty.
Basic Operation Performed on Queue are:
To insert element on a Queue using the following algorithm
void queue( )
{
if(Rear < 4)
{
printf(“Enter the number :”);
scanf(“%d” , &item);
if(front ==-1)
{
front=0;
rear=0;
}
else
{
rear = rear + 1
}
Queue[rear] =item;
}
else
Printf(“Queue is full”);
}
To delete element on a Queue using the following algorithm.
void delete( )
{
int item;
if(front!=-1)
{
item = queue[front];
if (front == rear)
{
front = -1;
rear =-1;
}
else
front = front+1;
print(“No deleted is = %d, item”);
}
else
printf(“Queue is empty”);
}
Listing: Following program is showing implementation of a Queue using array data structure
/*
* C Program to Implement a Queue using an Array
*/
#include <stdio.h>
#define MAX 50
int queue_array[MAX];
int rear = - 1;
int front = - 1;
main()
{ int choice;
while (1) {
printf("1.Insert element to queue \n");
printf("2.Delete element from queue \n");
printf("3.Display all elements of queue \n");
printf("4.Quit \n");
printf("Enter your choice : ");
scanf("%d", &choice);
switch (choice)
{
case 1:
insert();
break;
case 2:
delete();
break;
case 3:
display();
break;
case 4:
exit(1);
default:
printf("Wrong choice \n");
} /*End of switch*/
} /*End of while*/
} /*End of main()*/
insert()
{
int add_item;
if (rear == MAX - 1)
printf("Queue Overflow \n");
else
{
if (front == - 1)
/*If queue is initially empty */
front = 0;
printf("Inset the element in queue : ");
scanf("%d", &add_item);
rear = rear + 1;
queue_array[rear] = add_item;
}
} /*End of insert()*/
delete()
{
if (front == - 1 || front > rear)
{
printf("Queue Underflow \n");
return ;
}
else
{
printf("Element deleted from queue is : %d\n", queue_array[front]);
front = front + 1;
}
} /*End of delete() */
display()
{
int i;
if (front == - 1)
printf("Queue is empty \n");
else
{
printf("Queue is : \n");
for (i = front; i <= rear; i++)
printf("%d ", queue_array[i]);
printf("\n");
}
} /*End of display() */
Output:
1.Insert element to queue
2.Delete element from queue
3.Display all elements of queue
4.Quit
Enter your choice : 1
Inset the element in queue : 10
1.Insert element to queue
2.Delete element from queue
3.Display all elements of queue
4.Quit
Enter your choice : 1
Inset the element in queue : 15
1.Insert element to queue
2.Delete element from queue
3.Display all elements of queue
4.Quit
Enter your choice : 1
Inset the element in queue : 20
1.Insert element to queue
2.Delete element from queue
3.Display all elements of queue
4.Quit
Enter your choice : 1
Inset the element in queue : 30
1.Insert element to queue
2.Delete element from queue
3.Display all elements of queue
4.Quit
Enter your choice : 2
Element deleted from queue is : 10
1.Insert element to queue
2.Delete element from queue
3.Display all elements of queue
4.Quit
Enter your choice : 3
Queue is :
15 20 30
1.Insert element to queue
2.Delete element from queue
3.Display all elements of queue
4.Quit
Enter your choice : 4