Backtracking

When we are solving a problem using recursion, we break the given problem into smaller ones. Let's say we have a problem A and we divided it into three smaller problems B, C and D. Now it may be the case that the solution to A does not depend on all the three subproblems, in fact, we don't even know on which one it depends.

Let's take a situation. Suppose you are standing in front of three tunnels, one of which is having a bag of gold at its end, but you don't know which one. So you'll try all three. First, go in tunnel 1, if that is not the one, then come out of it, and go into tunnel 2, and again if that is not the one, come out of it and go into tunnel 3. So basically in backtracking, we attempt solving a subproblem, and if we don't reach the desired solution, then undo whatever we did for solving that subproblem, and try solving another subproblem.

Let's take a standard problem.
N-Queens Problem: Given a chess board having N×N cells, we need to place N queens in such a way that no queen is attacked by any other queen. A queen can attack horizontally, vertically and diagonally.

So initially we are having N×N unattacked cells where we need to place N queens. Let's place the first queen at a cell ((i,j), so now the number of unattached cells is reduced, and a number of queens to be placed is N−1. Place the next queen at some unattacked cell. This again reduces the number of unattached cells and number of queens to be placed becomes N−2.

Continue doing this, as long as following conditions hold.

• The number of unattached cells is not 0.

• The number of queens to be placed is not 0.

If the number of queens to be placed becomes 0, then it's over, we found a solution. But if the number of unattached cells becomes 0, then we need to backtrack, i.e. remove the last placed queen from its current cell, and place it at some other cell. We do this recursively.
The complete algorithm is given below:

Here's how it works for N=4.

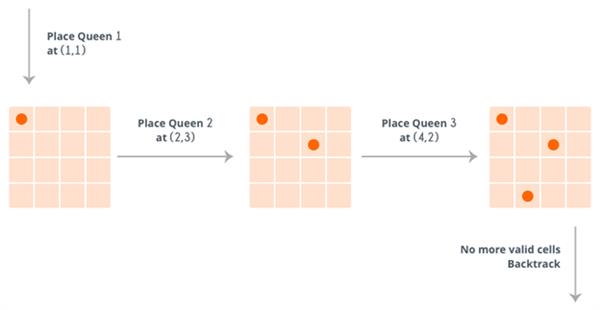
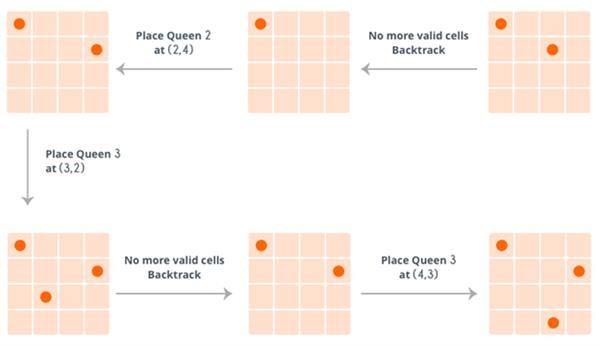
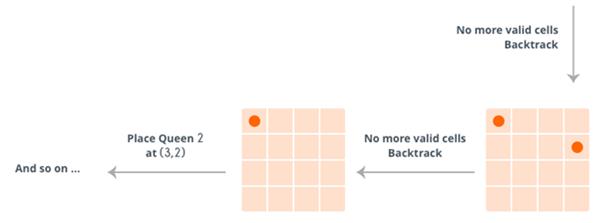
So, at the end it reaches the following solution:

So, clearly, the above algorithm tries solving a subproblem, if that does not result in the solution, it undoes whatever changes were made and solve the next subproblem. If the solution does not exist (N=2), then it returns false.