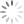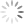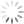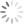GRAPHS

Graphs have found application in subjects like Geography, Chemistry and Engineering Sciences. They are also widely used in solving games and puzzles. In computer Science, graphs are used in many areas one of which is computer design. In day-to-day applications, graphs find their importance as representations of many of physical structure.

The graph theory helps us to solve problems like:

• How many colors do we need to color a map so that every pair of countries with a border in common has different colors?

• Given a map of several cities and the reach between them, it is possible for a traveling salesman to visit each of the cities exactly ones ?

DEFINING GRAPH

A graph G consists of a set V of vertices (nodes) and a set E of edges (arcs). We write G = (V , E), V is a finite and non-empty set of vertices. E is a set of pairs of vertices, their pairs are called edges.

Therefore, 

V (G), read as V of G, is a set of vertices 
and 
E (G), read as E of G, is a set of edges. 

An edge e=(v,w), is a pair of vertices v and w and is said to be incident with v and w.

Above figure shows a sample graph, for which 
V (G) = {v1, v2, v3, v4, v5} and
E (G) = {e1, e2, e3, e4, e5}

i.e., there are five vertices and five edges in the graph.

A graph may be graphically also represented as: 

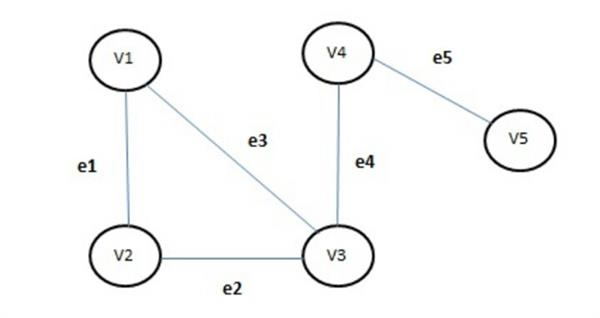
We have numbered the nodes as 1,2,3,4 and 5. Therefore 
V (G) = (1, 2, 3, 4, 5) and E (G) = {(1,2),(2,4),(2,3),(1,4),(1,5),(4,5),(3,4)} 

You may notice that the edge incident with node 1 and node 2 is written as (1,2); we could also have written (2,1) instead of (1,2). This is same for all other edges. We may say that ordering of vertices is not significant here in case of undirected graph. 

In an undirected graph, pair of vertices representing any edge is unordered. Thus (v,w) and (w,v) represent the same edge. In the directed graph each edge is an ordered pair of vertices i.e., each edge is represented by a directed pair. If e = (v,w), then v is initial vertex and w is final vertex. Subsequently (v,w) and (w,v) represent two different edges.

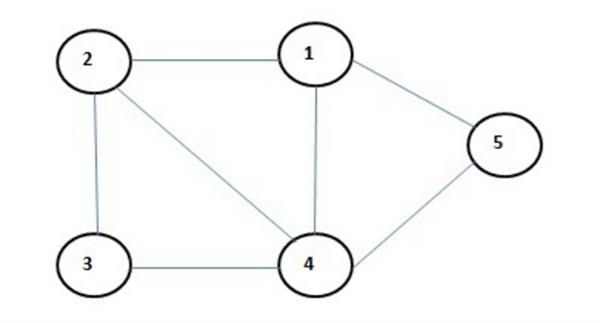
A directed graph may be pictorically represented as in figure.
The direction is indicated by an arrow.

The set of vertices for this graph is 
V (G) = (1,2,3,4) 
and the set of edges would be 
E (G) = {(1,2),(1,3),(1,4),(4,3),(3,2)} 

BASIC TERMINOLOGY

Adjacent Vertices: Vertex v1 is said to be adjacent to a vertexv2 if there is an edge (v1,v2) or (v2,v1). 
Let us consider the graph in the figure.

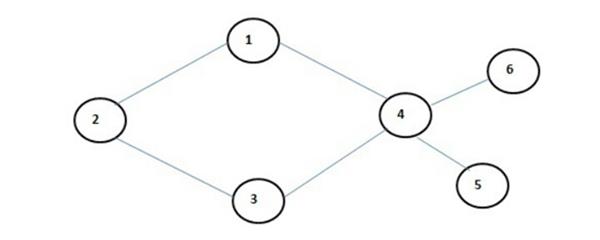
Vertices adjacent to node 2 are 1 and 3 and that to node 4 are 1,3,6 and 5. 

Path: A path from vertex w is a sequence of vertices, each adjacent to the next. Consider the above example again 1,2,3 is a path and 1,4 and 3 is also a path. 

Cycle: A cycle is a path in which first and last vertices are same. In the above example (1,2,3,4,1) is a cycle. 

Connected graph: A graph is called connected if there exists a path from any vertex to any other vertex. These are graphs which are unconnected. Consider the graph in Figure. 

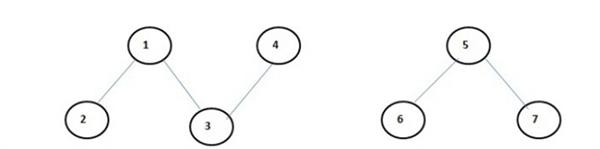
It is an unconnected graph. You may say that these are two graphs and not one. But it is one graph having two unconnected components, it is an unconnected graph. 
So far we have talked about paths, cycles, and connectivity of undirected graph. In a digraph, the path is called a directed path and cycle is called asdirected cycle. 

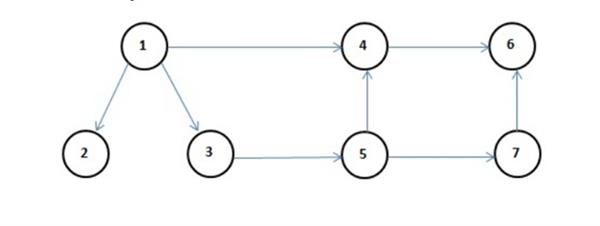
There is no directed cycle in the above graph. You may verify the above statements. A diagraph is called strongly connected if there is a directed path from any vertex to any other vertex. 

Consider the graph below in the figure. 

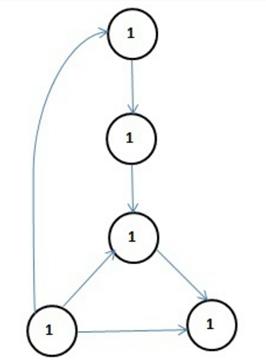
There does not exist a directed graph from vertex 1 to vertex 4, also from vertex 5 to other vertices and so on. Therefore, it is a weekly connected graph. To make it strongly connected there are certain changes that are required given as above in figure. 

Degree: The number of edges incident on a vertex determines its degree. The degree of vertex u is written as a degree(u). If degree(u)=0, this means that vertex u does not belong to any edge then vertex u is called isolated vertex. 

In a directed graph (Digraph), we attach an indegree and an outdegree to each of the vertices. 

Complete graph: A graph G is said to complete or fully connected if there is path from every vertex to every other vertex. A complete graph with n vertices will have n(n-1)/2 edges. 

Weighted graph: A graph is said to be weighted graph if every edge in the graph is assigned some weight or value. The weight of the edge is a positive value that may be representing the cost of moving along the edge or distance between the vertices. 

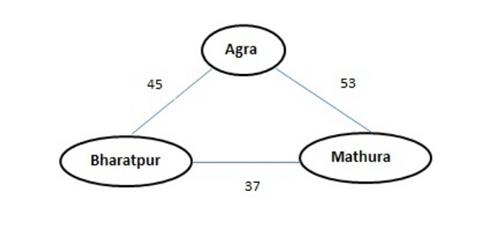
In the above figure, we mentioned the distance between Agra and Bharatpur as 45 km and Agra and Mathura is 53 km. 

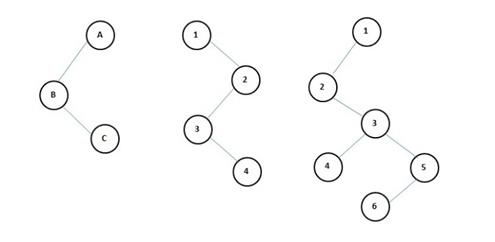
Tree: A graph is a tree if it has two properties:

• It is connected, and

• There is no cycle in the graph

The following graphs are Tree: 

Graph Representations

Graph data structure is represented using following representations.

• Adjacency Matrix

• Incidence Matrix

• Adjacency List

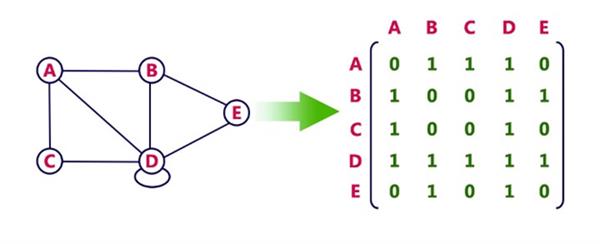
Adjacency Matrix

In this representation, a graph can be represented using a matrix of size total number of vertices by a total number of vertices. That means if a graph with 4 vertices can be represented using a matrix of 4 × 4 class. In this matrix, rows, and columns both represent vertices. This matrix is filled with either 1 or 0. Here, 1 represents there is an edge from row vertex to column vertex and 0 represents there is no edge from row vertex to column vertex.

For example, consider the following undirected graph representation.

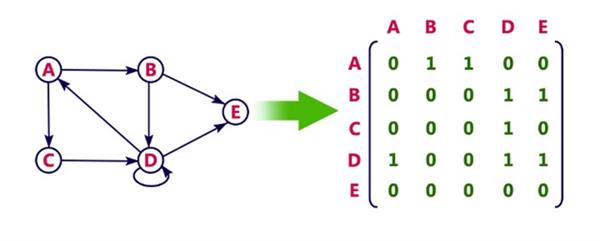
Directed graph representation.

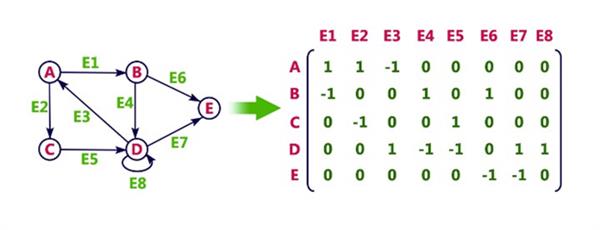
Incidence Matrix

In this representation, a graph can be represented using a matrix of size total number of vertices the y total number of edges. That means if a graph with 4 vertices and 6 edges can be represented using a matrix of 4X6 class. In this matrix, rows represent vertices and columns represents edges. This matrix is filled with either 0 or 1 or -1. Here, 0 represents row edge is not connected to column vertex, 1 represents row edge is connected an outgoing edge to column vertex and -1 represents row edge is connected as an incoming edge to column vertex.

For example, consider the following directed graph representation.

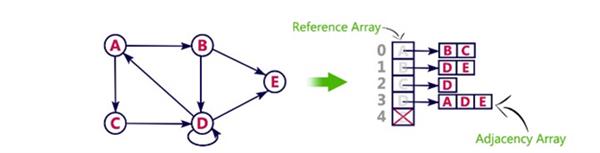
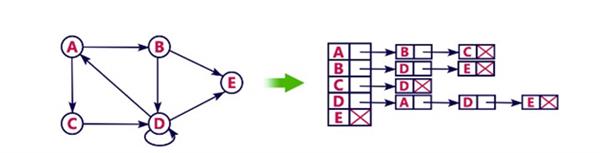
Adjacency List

In this representation, every vertex the f graph contains list of its adjacent vertices. For example, consider the following directed graph representation implemented using g linked list.

This representation can also be implemented using an array as follows.