Multi-Dimensional Array

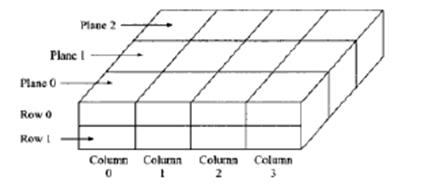
The arrays can also have more than two dimensions. For example, a three dimensional array may be declared as.

int myarray[3][2][4];

An element of this array is referenced by three subscripts. The first specifies the plane number, the second specifies the row number and the last one is column number. Such an array is useful when the value is determined by three inputs.

The number of elements in any array is the product of the ranges of all its dimensions. For example, myarray contains 3*2*4 = 240 elements. The int myarray[3][2][4]; can be represented as shown as