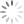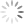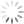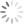Heap Sort

Heap sort is based on tree structure that reflects a particular order of a corporate hierarchy. Heap sort proceeds in two phases:

• The entries are arranged in the list satisfying the requirements of a heap.

• We repeatedly remove the top of the heap and promote another entry to take its place.

In the second phase, we recall that the root of the tree which is the first entry of the list as well as top of the heap has the largest key. This key belongs to the end of the list.

Algorithm:

Step1: Consider the values of the elements as priorities and build the heap tree.

Step2: Start deleteMin operations, storing each deleted element at the end of the heap array.

After performing step 2 , the order of the elements will be spposite to the order in the heap tree. Hence, if we want elements to be sorted in ascending order, we need to build the heap tree in descending order the greatest element will have the highest priority.

Example : 

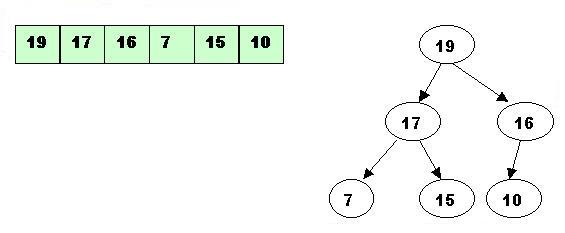
Here is the array: 15 19 10 7 17 6

Step1: the array represented as a tree, complete but not ordered.

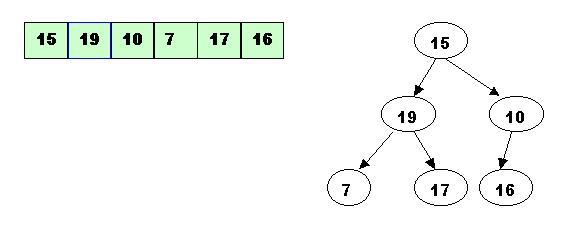
Step2: Start with the rightmost node at height 1-the node at position 3 =Size/2.It has one greater child and has to be percolated down.

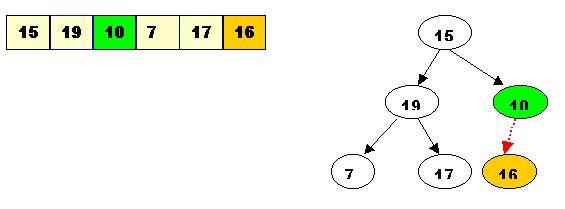
Step3: After processing array[3] the situation is:

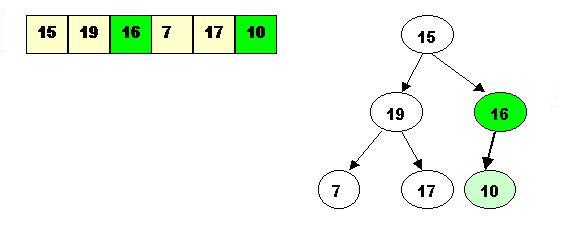
Step4: Next comes array[2], Its children are smaller, so no percolation is needed.

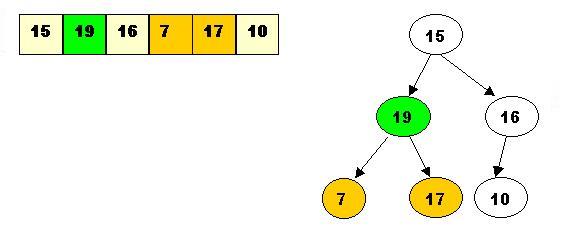
Step3: The last node to be processed is array[1]. Its left child is the greater of the children the item at array[1] has to be percolated down to the left, swapped with array[2].

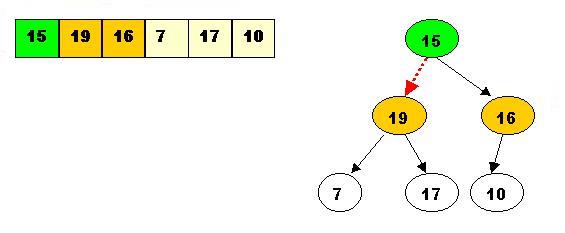
Step4: As a result the situation is:

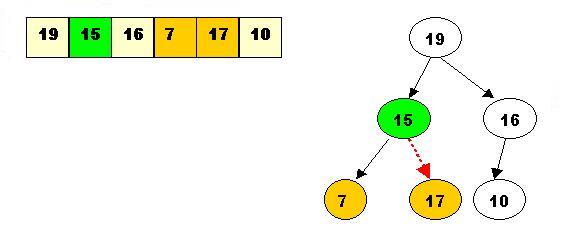
Step5: The children of array[2] are greater, and item 15 has to be moved down further, swapped with array[5].