- INTRODUCTION TO DS
- ALGORITHMS
- ASYMPTOTIC ANALYSIS
- DYNAMIC PROGRAMMING
- DIVIDE AND CONQUER
- Arrays
- Linked List
- STACK
- EXPRESSION PARSING
- Queue
- GRAPHS
- TREE
- SEARCHING TECHNIQUES
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- Binary Search
- Indexed Sequential Search
- Breadth First Search
- Depth First Search
- Interpolation Search
- Complexity
- SORTING
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Bubble Sort
- Selection Sort
- Quick Sort
- Insertion Sort
- Radix Sort
- Merge Sort
- Shell Sort
- Heap Sort
- Complexity
- Recursion
- Backtracking
- Hashing
Binary Tree
A binary tree is a finite set of data items which is either empty or consists of a single item called the root and two disjoint binary trees called the left subtree and right subtree.
A binary tree is a very important and the most commonly used non-linear data structure. In a binary tree, the maximum degree of any node is at most two. That means, there may be a zero degree node or a one-degree node and two-degree node.
A binary tree can also be defined as follows:
- A binary tree is an empty tree.
- A binary tree consists of a node called root, a left subtree and a right subtree both of which are binary trees once again.
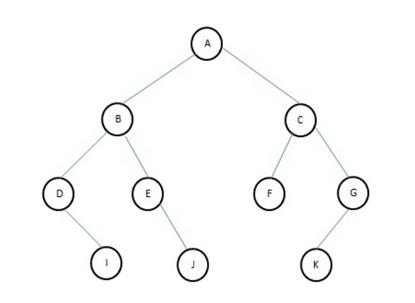
STRICTLY BINARY TREES
If every non-terminal node in a binary tree consists of the non-empty left subtree and right subtree, then such a tree is called strictly binary tree.
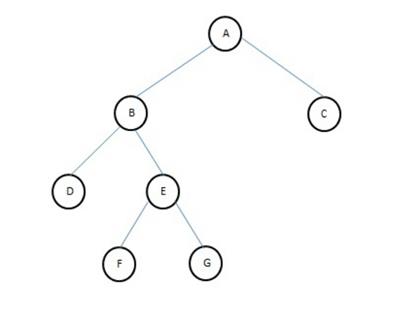
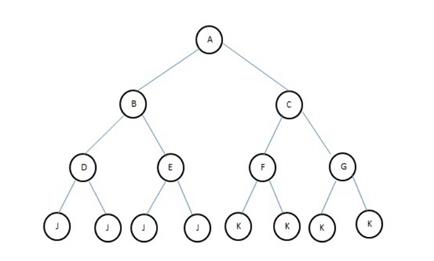
COMPLETE BINARY TREES
A binary tree with n nodes and of depth d is a strictly binary tree all of whose terminal nodes are at level d. In a complex binary tree, there is exactly one node at level 0, two nodes at level 1, and four nodes at level 2 and so on.